线段树是一种比较强大的数据结构，主要用于在动态更新区间的情况下，保持查找和更新在O(log(n))级别的时间复杂度。虽然它不是一颗完全二叉树，但构造时按照完全二叉树进行构树，没有的话叶结点留空，数组按完全二叉树构造：对于父节点编号为x，其左右儿子结点分别为：2x和2x+1。如下图所示：

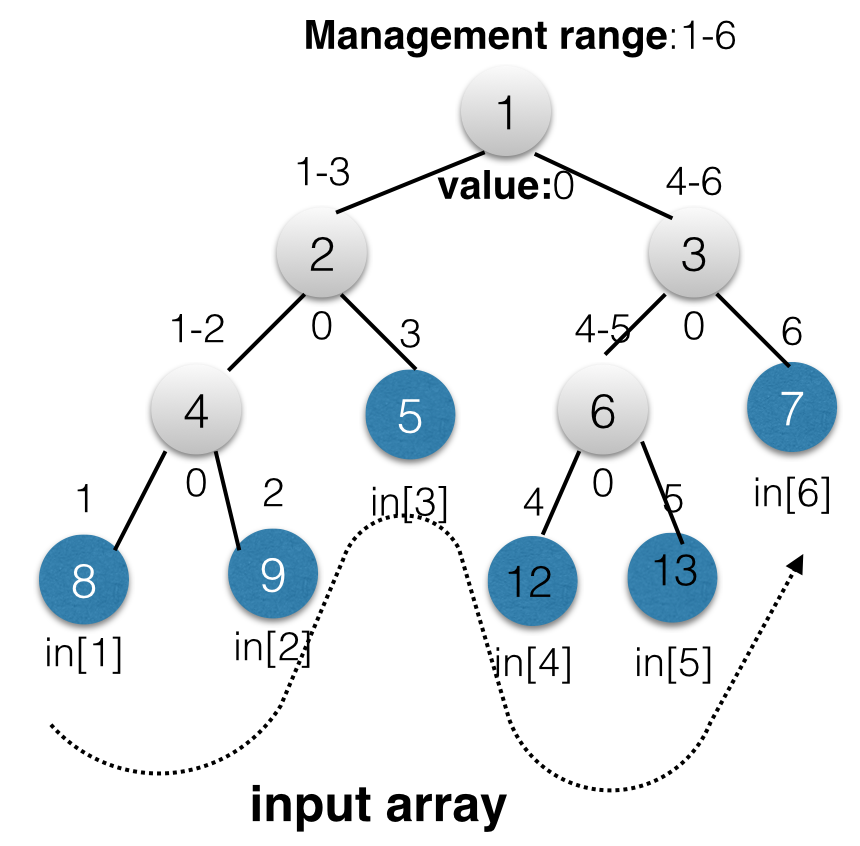
  Management range表示该结点的『负责输入结点』的范围，1-3表示负责输入结点1，2和3，即：in[1]，in[2]和in[3]。value值表示初始化值，刚开始构造时值为0，构造之后的值为子结点的『某种运算』结果：比如，对于『求区间最小值』，则value(4) = min(value(8), value(9))，value(1) = min(value(2), value(3))`，这个在图中未标出来。图中蓝色结点为输入的结点，虚线方向为数组的输入方向（所有叶子结点）。
  模板如下，为区间求和，单点+1更新：

#define le(x) x << 1
#define ri(x) x << 1 | 1
#define lson l, m, le(rt)
#define rson m + 1, r, ri(rt)

const int SIZE = 5000;

int num[SIZE << 2];  
int x[SIZE];

void push_up(int rt)  
{
    num[rt] = num[le(rt)] + num[ri(rt)];
}

void build(int l, int r, int rt) {  
    int m = (l + r) >> 1;  
    if(l == r) {  
        scanf("%d", &num[rt]);
        return ;  
    }  
    build(l, m, le(rt));  
    build(m + 1, r, ri(rt));  
    push_up(rt);  
}

void update(int p, int l, int r, int rt)  
{
    int m;
    if(l == r) {
        num[rt] ++;
        return ;
    }
    m = (l + r) >> 1;
    if(p <= m)
        update(p, lson);
    else
        update(p, rson);
    push_up(rt);
}

//[L,R]: query interval
int query(int L, int R, int l, int r, int rt)  
{
    int m, ret = 0;
    if (L <= l && r <= R) {
        return num[rt];
    }
    m = (l + r) >> 1;
    if (L <= m)
        ret += query(L, R, lson);
    if (R > m)
        ret += query(L, R, rson);
    return ret;
}

  好吧，上题目吧。

1.hdu1166 敌兵布阵

  题意：给定n个数，有两种操作：1.单点更新 2.区间求和查询
  解题：裸题，上模板。

2.hdu1754 I Hate It

  题意：给定n个数，有两种操作：1.单点更新 2.区间最值查询
  解题：裸题，上模板。

------未完待续，太忙了，没时间刷题了